Projective Geometry: Transformations of Three Flags

Flags consist of a line and a point lying on the line. There exist different transformations of flags, such as the eruption flow. Here we present several visualizations of these transformations.

What are flags?

Let $\mathbb{RP}^2$ be the real projective plane. A flag is a tuple $(p, l)$ consisting of a point $p$ in $\mathbb{RP}^2$ and a projective line $l$ containing the point. Most of the time, we will only be considering a special case, positive tuples of flags. In fact, a lot geometric ideas only make sense in this case. We denote the set of positive $n$-tuples of flags by $\mathcal{F}^n_+$.

The action of the projective linear group $\mathbf{PGL}(3,\mathbb{R})$ on $\mathbb{RP}^2$ descends to an action on $\mathcal{F}^n_+$.

Visualizing the projective plane

The projective plane $\mathbb{RP}^2$ is an abstract mathematical object that has different equivalent definitions. How do we visualize this space?

Define the projective plane as the space of all straight lines through the origin of $\R^3$. We can visualize a big part of this space by projecting those lines to a plane: Choose a plane that has distance 1 from the origin. Every line that intersects with the plane will be represented by the intersection point, so we have a two-dimensional visualization of a chunk of $\mathbb{RP}^2$. The lines that don’t intersect with the plane (as they are parallel to the plane) are the infamous “points at infinity”.

Transformations of triples of flags

Definition of the Eruption Flow

The eruption flow is a flow on positive triples of flags which doesn’t come from the action of $\mathbf{PGL}(3,\mathbb{R})$. Nevertheless, it commutes with the action, and therefore also induces a flow on the orbit space. We define it as follows.

Let $(p_i,l_i)_{i=1,2,3}\in\mathcal{F}^3_+$ be a triple of flags. It is equivalent to a pair of nested triangles $\Delta=(p_1, p_2, p_3)$ and $\Delta'=(q_1, q_2, q_3)$ as can be seen in the figure below. This induces three quadrilaterals $Q_1, Q_2$ and $Q_3$.

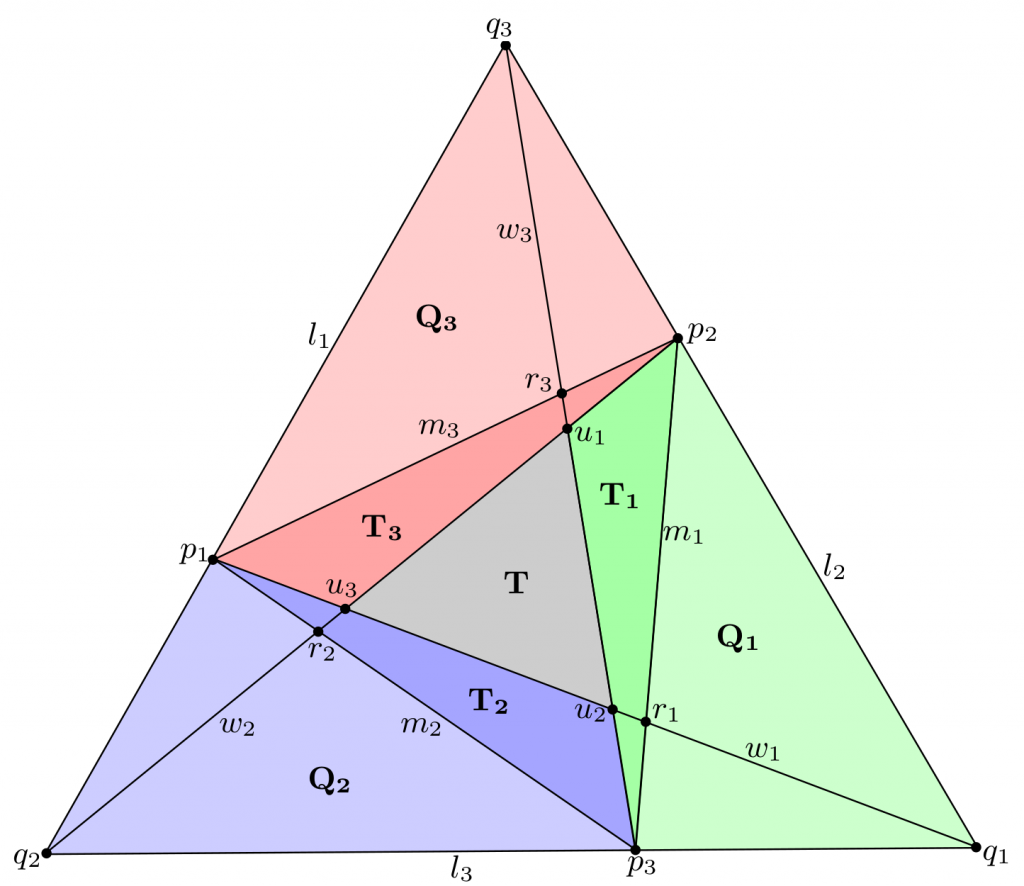
The flow is now defined by deforming each quadrilateral $Q_i$ with a different element of $\mathbf{PGL}(3,\mathbb{R})$, namely

where all matrices are written in a basis given by representatives of $q_1, q_2$ and $q_3$. In fact, this transformation leaves the points $q_i$ invariant. The transformed points $p_i(t)$ remain on the lines $l_i$, so the transformation gives us a pair of nested triangles $\Delta(t),\Delta'(t)$ equivalent to a triple of flags, as can be seen in the figure above.

Visualizations of the Eruption Flow

3D-printing the erupting volcano

In the 3D-printed model, the model height represents the progression of $t$, whereas each horizontal section (in green) is the transformed inner triangle $T(t)$ from the above decomposition. The grey base triangle is the triangle $\Delta'$.

Different fixed points of the eruption flow

The eruption flow can have different fixed points depending on how we apply the matrices $g_i(t)$. If we choose the points $q_i$ as basis points, these points will remain fixed. However, if we choose the points $p_i$, they will become the fixed points, and the $q_i$ will move. You can see the difference in the movies. This is not a grave difference as these two transformations only differ by a $t$-dependent element of $\mathbf{PGL}(3,\mathbb{R})$.

The red triangle is the triangle spanned by $u_i$, the blue triangle the one spanned by $p_i$, and the black triangle is spanned by $q_i$. The time represents the transformation parameter $t$.

Transforming a circle

Choose a projection of the projective plane under which the outer triangle $q_i$ and the middle triangle $p_i$ are both equilateral, and each point $p_i$ lies exactly in the middle of the line of the outer triangle. Then the inner triangle spanned by the $u_i$ is reduced to a point. In fact, it is the center of the triangle. We can look at the inscribed circle and watch its transformation under the eruption flow, which gives a good impression of the flow’s effect.

More on transformations of flags

We can also transform larger numbers of flags, see here for the eruption flow on four-tuples of flags, as well as other transformations: the bulge flow and the shear flow.

The mathematical information on this site is due to

Wienhard, A. & Zhang, T. (2017). Deforming convex real projective structures. math.GT; arXiV 1702.00580.