Projective Geometry: Transformations of Four Flags

What is a flag?

A flag consists of a line and a point lying on that line. We consider flags in the two-dimensional real projective space. This is a two-dimensional plane, but we “add” all the points at infinity, this means for each set of parallel lines, we add a point at infinity where all these lines intersect. By only choosing a part of this space, we can visualize it, see here for details. We will look at different transformations of four flags, the bulge flow, the shear flow and the eruption flow.

Transformations of four flags

The bulge flow and the shear flow are flows on tuples of four flags.

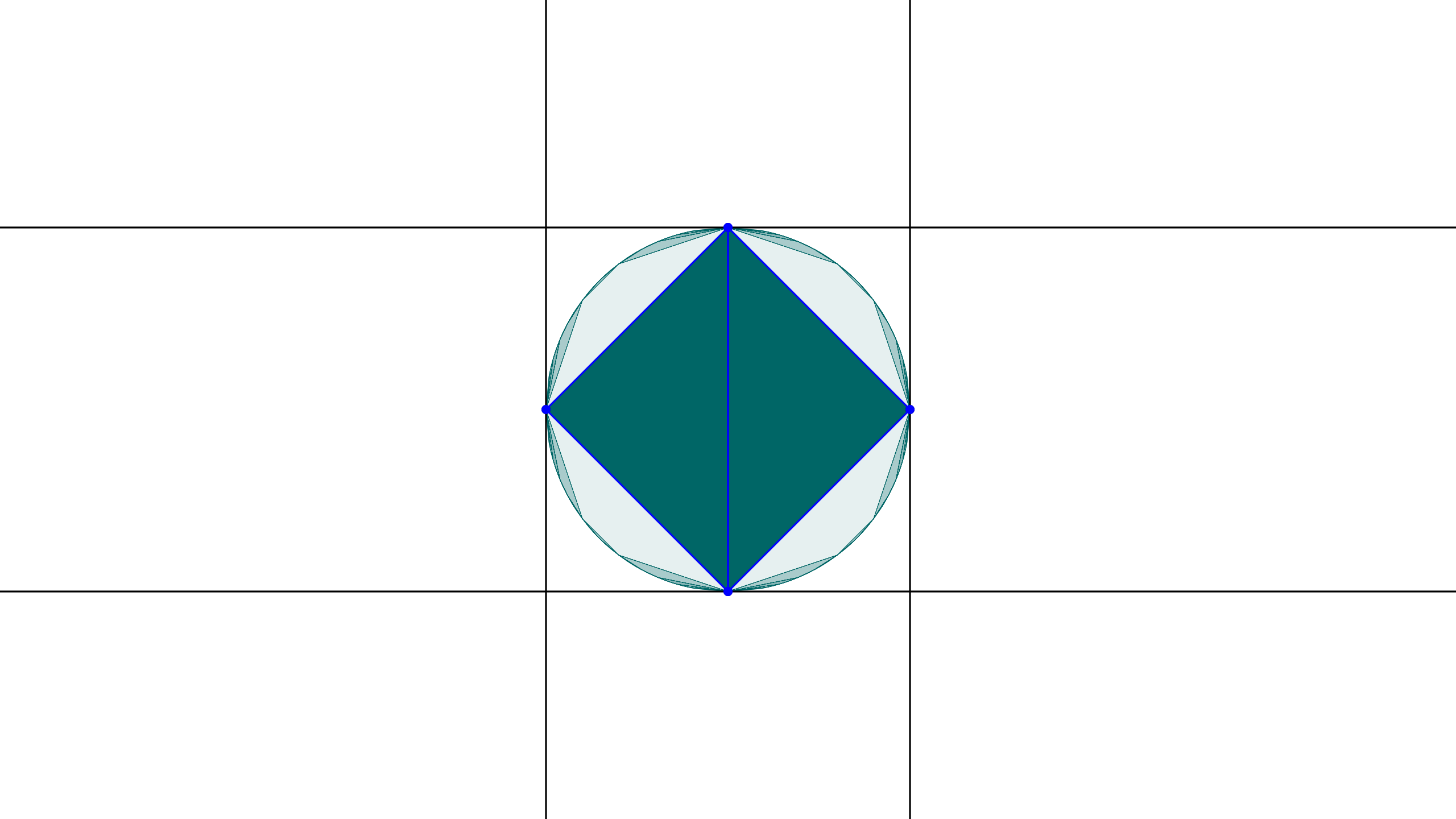
Consider a positive tuple (p_i,l_i)_{i=1,\ldots, 4}\in\mathcal{F}^4_+ of four flags. The intersection points of the lines span a quadrilateral. Similar to the eruption flow on three flags, the quadrilateral is divided into different areas, and we apply a matrix to each one of them.

Convex sets

In fact, a tuple of four flags defines two nested quadrilaterals: The outer quadrilateral is spanned by the intersection points q_i of the lines, the inner quadrilateral is spanned by the p_i. We can construct a convex set from the inner quadrilateral by reflecting it along each of it sides. We repeat this procedure up to infinity. By reflection, we mean a special kind of projective reflection: Imagine you are standing on train tracks and seeing a point v at the horizon where the parallel tracks meet. Imagine the quadrilateral lying on the ground. If you reflect it along one of its sides l, it will look different than its mere mirror image. This is due to the perspective. As a mathematical formula, we write this projective reflection as

where l(\cdot) is the linear form that defines the projective line l.

See down below for an image of this convex set.

Visualizations of the different flows

The bulge flow

In this movie, we see where the name bulge flow comes from. Depending on the choice of parameter, the initial quadrilateral bulges further and further to the right or to the left.

The shear flow

In this movie, we see why the shear flow is called that way. The left and the right point are twisted as if they were experiencing a shear force. Also note another interesting property of the shear flow. While two points in the middle remain fixed, the left and the right point will remain on ellipse segments at all times.

The convex set under the eruption flow

As explained before, we construct a convex set from a positive tuple of flags by reflecting the polygon along its sides. If we divide the polygon into triangles, we can transform each triangle using the eruption flow and see what happens to the convex set. This division into triangles can be seen as blue lines in the picture.

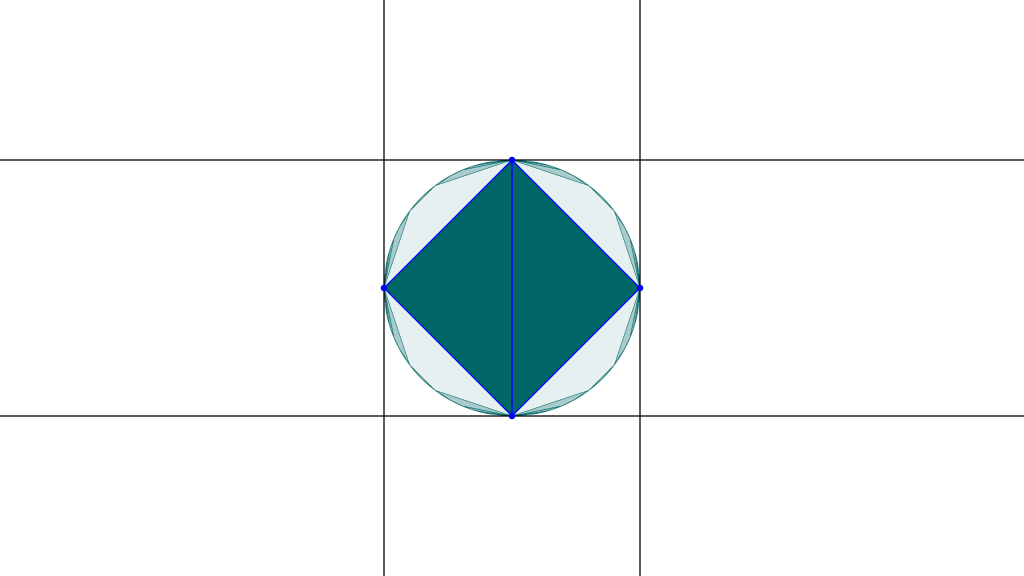
We now have different choices for applying the eruption flow. We could transform one of the triangles with a positive parameter, \phi_t, and the other one with a negative parameter \phi_{-t}. Instead, we could also transform both triangles with a positive parameter \phi_t and \phi_t.

The result looks quite different, see

in comparison to the following video.

Note that we usually retransform the whole image after each transformation with a projective transformation, i.e. an element of \mathbf{PGL}(3,\mathbb{R}), in order to keep the black lines fixed. If we don’t do this, the image quickly “explodes”, as can be seen below.

More on transformations of flags

The mathematical information on this site is due to

Wienhard, A. & Zhang, T. (2017). Deforming convex real projective structures. math.GT; arXiV 1702.00580.