Generating Highly Designable Proteins with Geometric Algebra Flow Matching

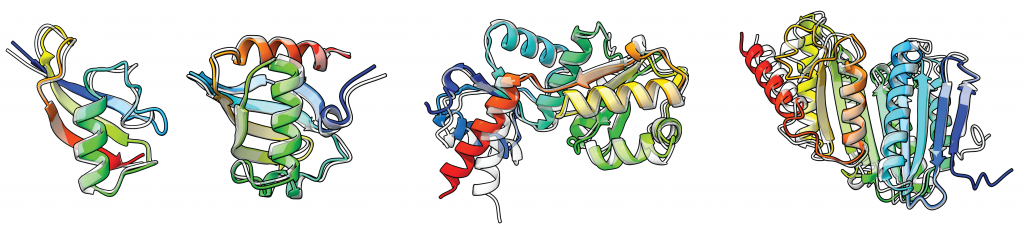
Generating structurally diverse and physically realizable protein backbones remains one of the grand challenges in protein design. We propose a generative model for protein backbone design utilizing geometric products and higher order message passing, which we call GAFL. In particular, we propose Clifford Frame Attention (CFA), an extension of the invariant point attention (IPA) architecture from AlphaFold2, in which the backbone residue frames and geometric features are represented in the projective geometric algebra [1]. This enables to construct geometrically expressive messages between residues, including higher order terms, using the bilinear operations of the algebra. We evaluate our architecture by incorporating it into the framework of FrameFlow [2], a state-of-the-art flow matching model for protein backbone generation. The proposed model achieves high designability, diversity and novelty, while also sampling protein backbones that follow the statistical distribution of secondary structure elements found in naturally occurring proteins, a property so far only insufficiently achieved by many state-of-the-art generative models.

Paper: https://arxiv.org/abs/2411.05238
Code: https://github.com/hits-mli/gafl

Background and Motivation

State-of-the-art methods typically represent the structure of a protein of N residues as an element of the group SE(3)^N, i.e. as a collection of N frames, each of which describes the position and orientation of an individual protein residue. By modeling a protein through the frames of its backbone, the task of protein structure generation essentially becomes to model the distribution of a set of frames, an inherently geometric problem. Most generative models for protein design use the gauge-invariant representation of AlphaFold2 in which the predicted frames are used as local coordinate frames, thus E(3)-equivariance of the feature representations is not required. We reasoned that the Projective Geometric Algebra (PGA) could provide a powerful framework for protein backbone design since any E(3) transformation of the protein backbone can be described as a set of repeated reflections within PGA (see figure below). The elements of PGA can encode the frames of a protein backbone as well as further geometric objects like points, lines and planes, which are well suited to capture the abstract geometry of α-helices and β-sheets.

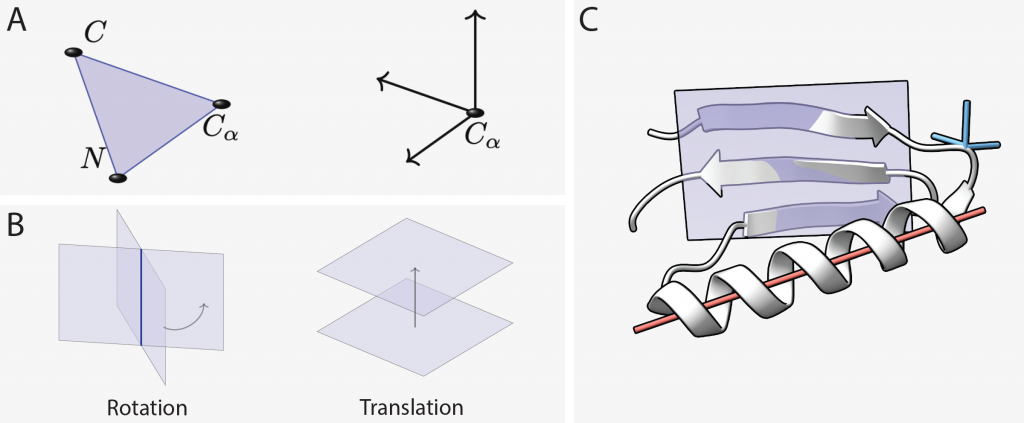
Geometric objects and operations central for protein structure can be expressed within PGA.
(A) Protein backbone residue with three backbone atoms represented by a coordinate frame. (B) In PGA, a frame can be represented via the geometric product of four planes. Two of the planes parameterize the frame’s rotation around their line of intersection, while the other two encode the frame’s translation along the separation vector between them. (C) An exemplary protein backbone structure containing an α-helix and a β-sheet. Lines (red), planes (violet) and Euclidean frames (blue) can all be embedded as elements of PGA, facilitating a geometric inductive bias for learning representations of the abstract geometry of the protein.

Clifford Frame Attention (CFA)

The original Invariant Point Attention (IPA) mechanism of AlphaFold [5] uses geometric node features in the form of 3D points for the calculation of attention scores and as queries, keys and values. The features are expressed in local coordinate frames, which allows the use of arbitrary layers without breaking equivariance. Messages between nodes are constructed as a linear combination of attention values, weighted by attention scores. While other generative models for protein design incorporate the original version of IPA directly, we propose to enhance its geometric expressivity by introducing PGA-valued multivector features and bilinear layers involving the geometric product inspired by [1], higher order messages and frames as node features.

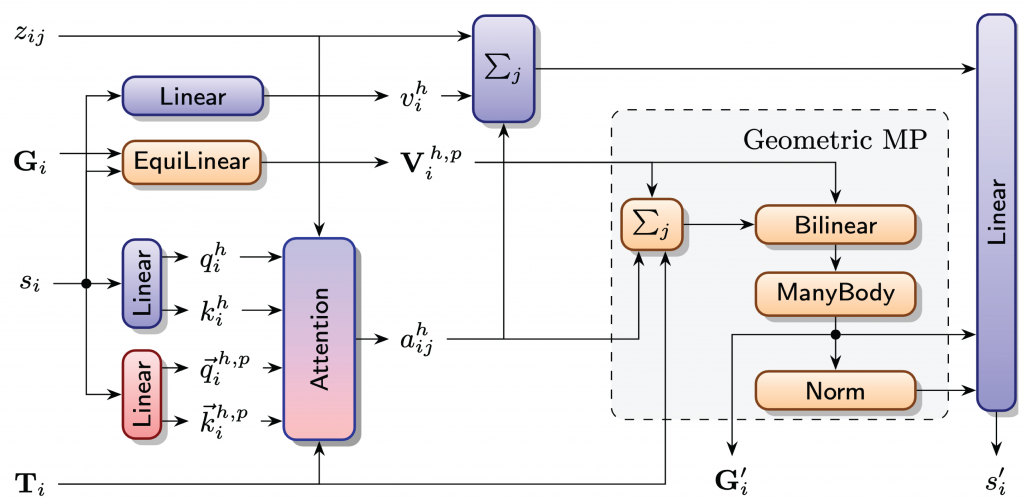
CFA enhances the geometric expressivity of AlphaFold’s Invariant Point Attention (IPA).
We extend point valued features in the original version of IPA by multivectors and further introduce geometric bilinears and higher order message passing. Blue nodes represent layers that process scalar information, red nodes represent layers that process point valued information and orange nodes represent layers that process PGA-valued features. The central innovation is the novel construction of geometric messages, summarized in the grey box.

Generating Protein Structures

We incorporate CFA into FrameFlow [2], an IPA-based state-of-the-art model for protein backbone generation. FrameFlow introduces Flow Matching on the manifold SE(3)^N, where the tangent vector field along geodesics between noise and data samples is learned. This allows to generate new samples by numerical integration of the predicted vector field.

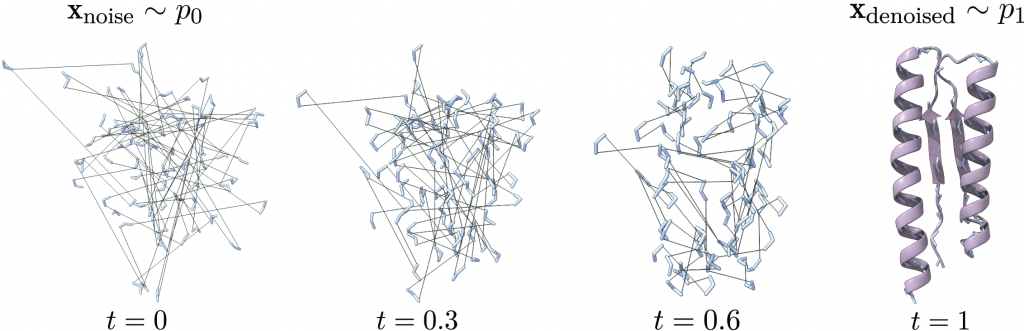
Visualization of a Flow Matching trajectory generated by GAFL.

Results

We train the proposed model, GAFL, on around 25,000 monomeric structures from the Protein Data Bank (PDB) and evaluate its performance in the established metrics designability, diversity and novelty, which reflect consistency, similarity between individual samples and similarity with the training set, respectively. Additionally, the mean content of α-helices and β-sheets in sampled backbones is calculated and compared to that of naturally occurring proteins. We compare GAFL with state-of-the-art models for protein structure generation such as FrameDiff [4], FoldFlow [6], FrameFlow [2] and RFdiffusion [3], the gold-standard in the field of protein design.

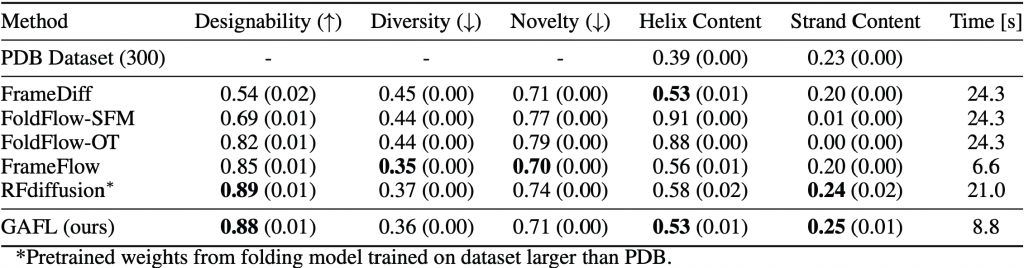
Performance of state-of-the-art models for protein structure generation at the task of generating backbones with 100 to 300 residues.

We find that GAFL can reliably generate designable, diverse and novel backbones while capturing the statistical distribution of secondary structure elements of natural proteins. In all metrics considered, GAFL outperforms both variants of FoldFlow and is better or as good as FrameDiff. GAFL also outperforms FrameFlow, which was trained on the same dataset, in terms of designability and, at the same time, achieves better secondary structure content. GAFL’s designability is only matched by RFdiffusion, which is not directly comparable since it relies on pre-trained model weights from a folding model and has around three times more parameters. For diversity, novelty and helix content, GAFL performs better than RFdiffusion. We also observe that GAFL and FrameFlow can generate backbones around three times faster than the other evaluated models.

Bibtex

@inproceedings{wagnerseute2024gafl, title={Generating Highly Designable Proteins with Geometric Algebra Flow Matching}, author={Wagner, Simon and Seute, Leif and Viliuga, Vsevolod and Wolf, Nicolas and Gr{\"a}ter, Frauke and St{\"u}hmer, Jan}, booktitle={Thirty-eighth Conference on Neural Information Processing Systems}, year={2024} }

References

[1] Johann Brehmer et al. Geometric algebra transformer. In Advances in Neural Information Processing Systems, volume 37, 2023

[2] Jason Yim et al. Improved motif-scaffolding with SE(3) flow matching. Transactions on Machine Learning Research, 2024. ISSN 2835-8856.

[3] Joseph L Watson et al. De novo design of protein structure and function with rfdiffusion. Nature, pages 1–3, 2023

[4] Jason Yim et al. Se (3) diffusion model with application to protein backbone generation. arXiv preprint arXiv:2302.02277, 2023.

[5] John Jumper et al. Highly accurate protein structure prediction with AlphaFold. Nature, 596(7873):583–589, August 2021.

[6] Joey Bose et al. SE(3)-stochastic flow matching for protein backbone generation. In The Twelfth
International Conference on Learning Representations, 2024.