Comparing Hyperbolic and Euclidean Geometry
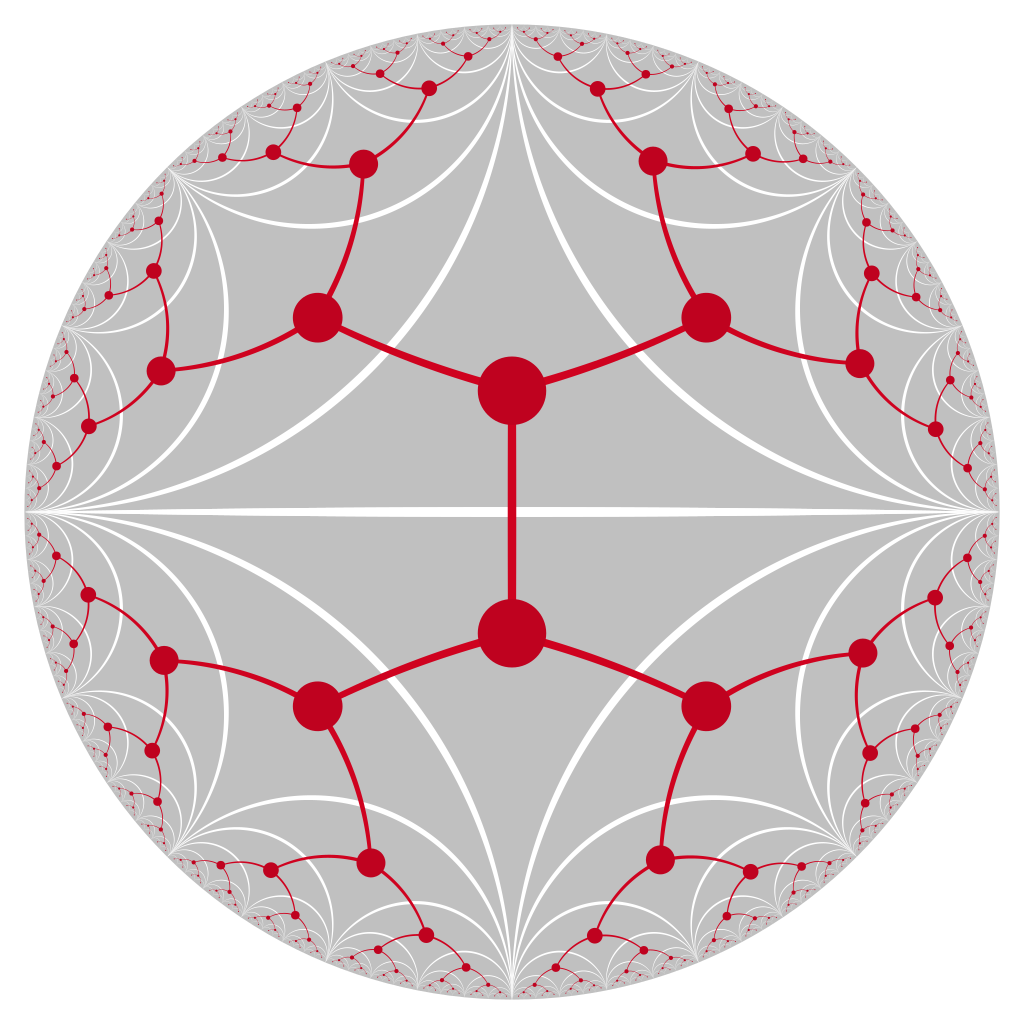
Tesselations of the euclidean and the hyperbolic plane
Hyperbolic and euclidean geometry have a quite distinct taste and are very different to each other. A good way to see this is a comparison of tilings, or tesselations, of these two geometries. Consider a tiling of the euclidean plane by squares, and a tiling of the hyperbolic plane by ideal triangles. We will then draw a graph that visualizes which tiles are adjacent to one another. In case of euclidean geometry, this is a simple grid. However, in the case of hyperbolic geometry, it becomes a tree that is getting infinitely finer in any direction.
We used the Poincaré disc model for visualizing the hyperbolic plane.

Tesselation of the Euclidean plane using squares. 
Graph (in red) visualizing which tiles are adjacent to one another.

Tesselation of the hyperbolic plane using ideal triangles. 
Graph (in red) visualizing which tiles are adjacent to one another.
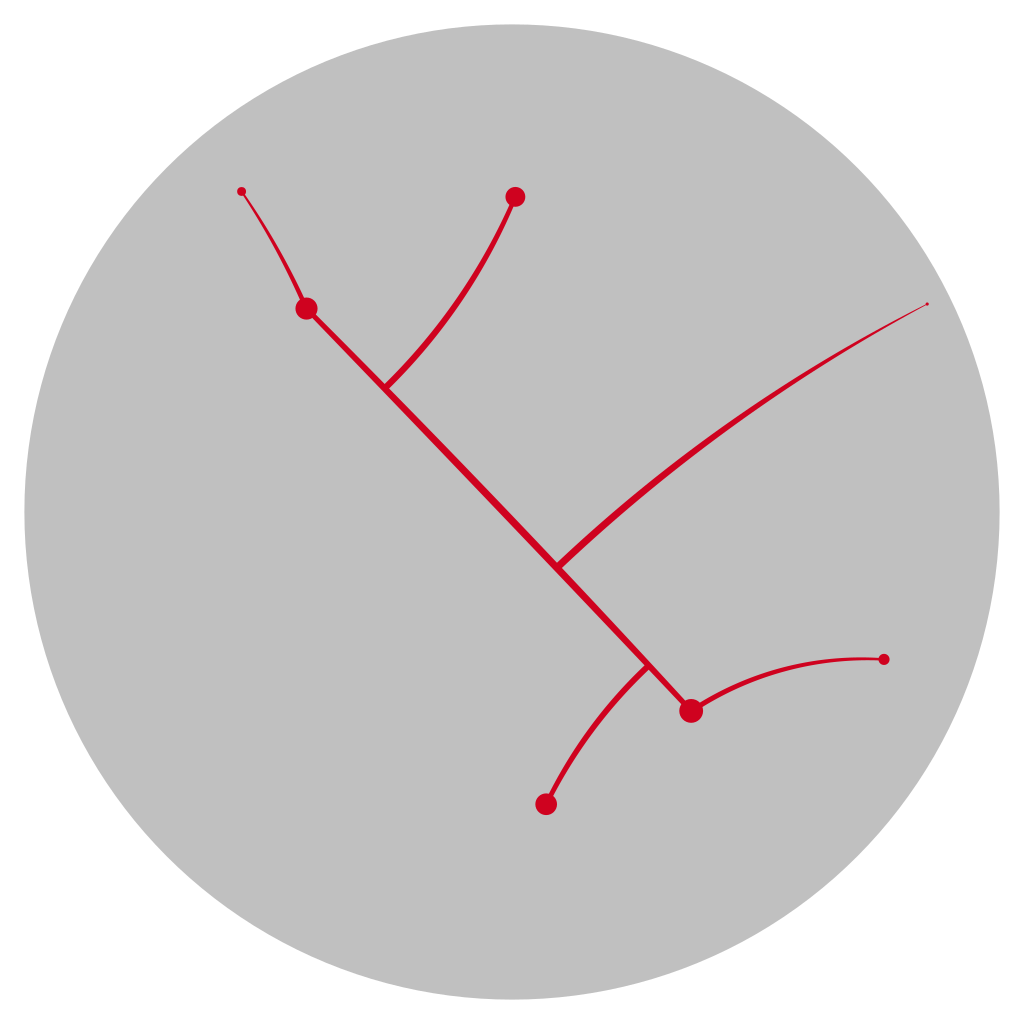
The approximating graph in the hyperbolic plane
Pick a finite set of points in the hyperbolic plane, a “point cloud” so to speak. The “shortest path”, or more correctly a geodesic between these two points is a circle segment in the Poincaré disc model. Connecting each pair of points by the corresponding geodesic gives us quite a network of lines. It is a nice fact that this can be simplified by an approximating tree: There is a graph whose edges are geodesics and whose nodes contain all the points of our point cloud, such that going along the edges of the graph from one point to another is not “a lot further” than going the direct way. The distance differs by an error which only depends on the number of points n:
d_\mathrm{tree}(x, y) \leq d(x,y) + f(n).We used a very simple algorithm for constructing this graph: The first edge is simple the geodesic connecting the first two points. After that, pick a point in the cloud that is not yet connected to the graph, and add the edge between this point and the point on the graph that is closest to this point. The result can be seen below.
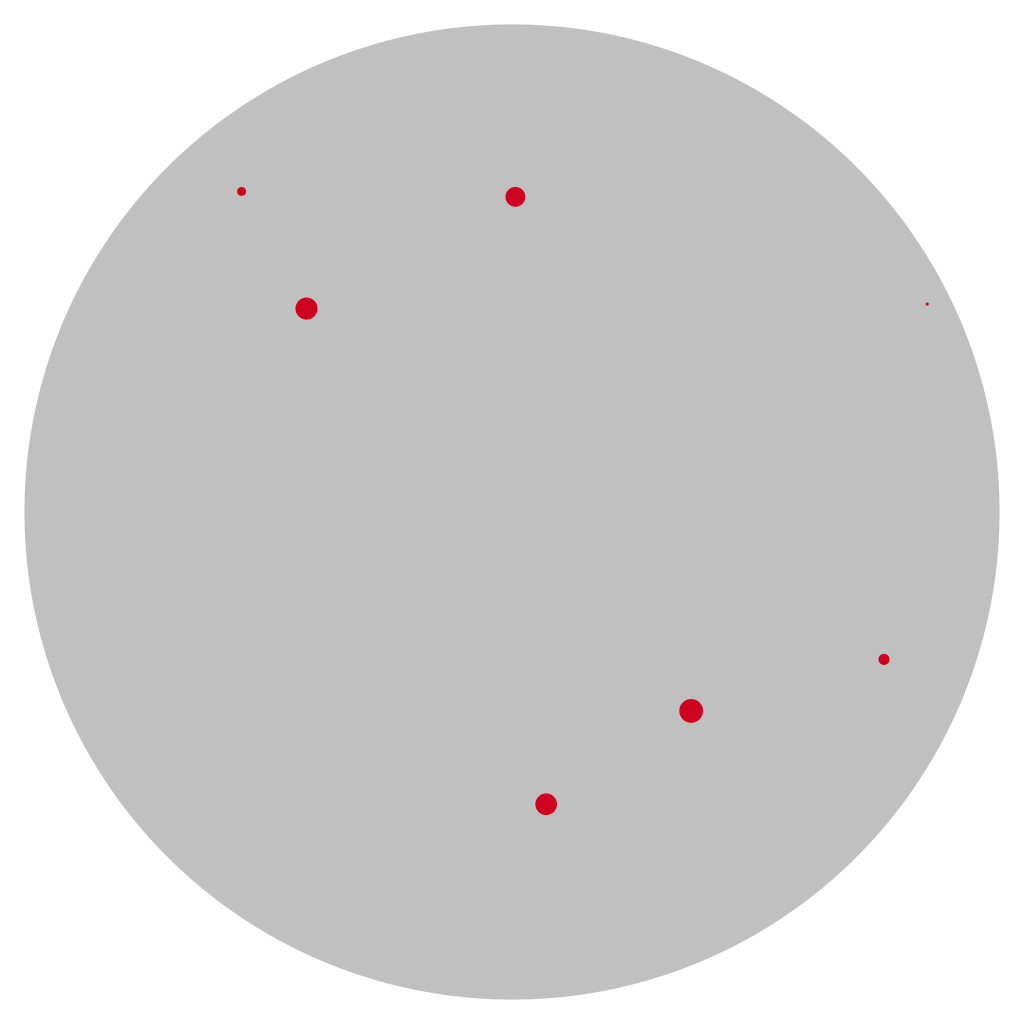
A point cloud in the hyperbolic plane. 
All the geodesics connecting pairs of points, and the approximating graph for comparison.