3D printers at HITS

Due to the necessary formalism and high level of abstraction, pure mathematics can be hard to grasp for people from different specializations. Additionally, research is not constrained to our three familiar dimensions. This even further impedes intuitive understanding. To address that, we want to make geometry “palpable”. With aid of two 3D printers we demonstrate mathematical concepts such as knots, curved spaces or rolling objects.

The 3D printer thus does not only contribute to science communication but also supports the researchers in their spatial sense.

On this page you can find models and explanations for these projects which require very different levels of prior knowledge.

What type of data do we feed to the 3D-printer? Geometric objects in 3-dimensional Euclidean space are defined by the collection of their points and the relative positions of those points. Even if we can abstractly define such geometric objects with infinite precision, this does not mean that we are able to visualize them with the same precision.

A ‘manifold’ is defined by its property that every point on this object possesses at least a small neighborhood that looks like a linear space, even though the manifold as a whole is very different from a linear space.

When we want to collect all the information described by a manifold we need to prescribe the way all of these infinitely many small linear neighbourhoods are glued together to result the non-linear geometric object. This process is possible in terms of formuli, but a computer visualising this object needs the information to be fed in the form of a finite collection of finite sequences of binary digits.

This leads us to a compromise, reducing this infinite amount of information into something finite. The compromise is that we will be approximating the smooth geometric object, i.e. the manifold, by a rougher picture of its true nature. Geometers call this process in 3-dimensions a triangulation.

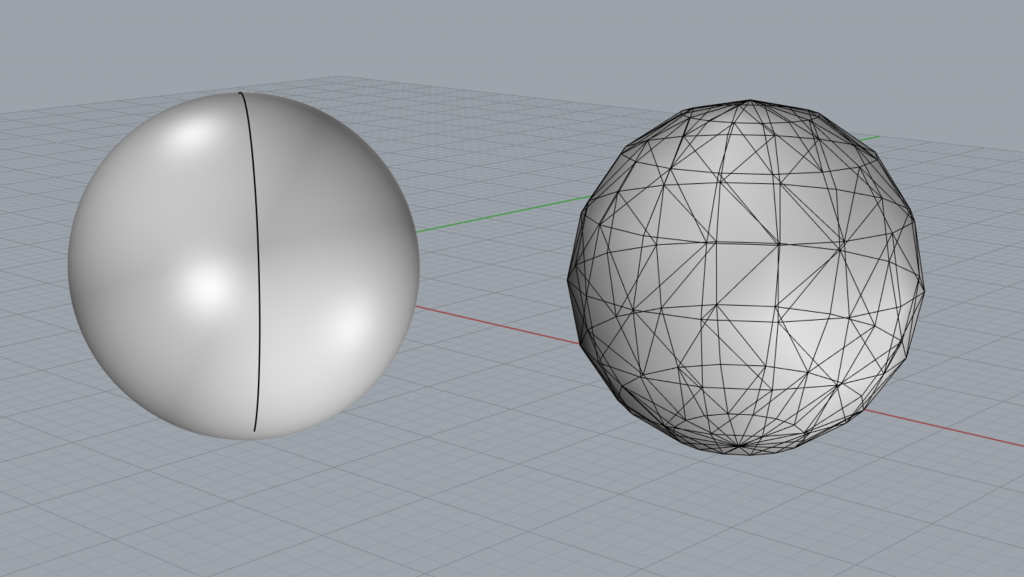
Under this procedure we turn the infinitesimal neighborhoods into small flat triangles of finite area, thereby creating a mesh. As the triangles have finite area, we have finitely many triangles as well as finitely many distinguished points, these being the edges of the triangles, which are connected by straight lines and these finitely many lines span linear spaces. Therefore, we obtain finitely many binary sequences of finite length, which a computer can comprehend with, and construct an image.

Before feeding the visualized data to the 3D-printer there is another step to be performed. Namely, we need to slice the 3D object to a collection of layers. The 3D printer melts small portions of polymer and deposits the material layer-wise on a build plate. The slicing function defines the shape of each layer and stacks them together along the vertical axis with respect to the build plate, to build the complete 3D object. Now our 3D printer is ready for action.