Projektive Geometrie: Transformationen von drei Fahnen

Fahnen bestehen aus einer Geraden und einem Punkt, der auf der Geraden liegt. Es gibt verschiedene Transformationen von Fahnen, wie z.B. den Eruptionsfluss. Hier zeigen wir verschiedene Visualisierungen dieser Transformationen.

Was sind Fahnen?

Sei \mathbb{RP}^2 die reelle projektive Ebene. Eine Fahne ist ein Tupel (p, l), das aus einem Punkt p in \mathbb{RP}^2 und einer projektiven Gerade l besteht, die diesen Punkt enthält. Zumeist werden wir einen Spezialfall betrachten, nämlich positive Tupel von Fahnen. In der Tat ergeben viele geometrische Betrachtungen nur in diesem Fall Sinn. Wir bezeichnen die Menge positiver n-Tupel von Fahnen als \mathcal{F}^n_+.

Die Wirkung der projektiven linearen Gruppe \mathbf{PGL}(3,\mathbb{R}) auf \mathbb{RP}^2 lässt sich zu einer Wirkung auf \mathcal{F}^n_+ einschränken.

Visualisierungen der projektiven Ebene

Die projektive Ebene \mathbb{RP}^2 ist ein abstraktes mathematisches Objekt, dass sich auf verschiedene, zueinander äquivalente Arten definieren lässt. Wie visualisieren wir diesen Raum?

Definiere die projektive Ebene als Menge aller Ursprungsgeraden im \R^3. Wir können einen großen Teil dieses Raums visualisieren, indem wir die Geraden auf eine Ebene projizieren: Wähle eine Ebene mit Abstand 1 zum Ursprung. Jede Gerade, die diese Ebene schneidet wird von ihrem Schnittpunkt mit der Ebene repräsentiert, sodass wir eine zweidimensionale Darstellung eines Stücks des \mathbb{RP}^2 erhalten. Die Geraden, die sich nicht mit der Ebene schneiden, entsprechen den berüchtigten „Punkten im Unendlichen“.

Transformationen von Fahnentripeln

Definition des Eruptionsflusses

Der Eruptionsfluss (engl. eruption flow) ist ein Fluss auf positiven Tripeln von Fahnen, der nicht von der Wirkung der \mathbf{PGL}(3,\mathbb{R}) induziert wird. Nichtsdestotrotz kommutiert er mit der Wirkung und induziert daher auch einen Fluss auf dem Orbitraum. Wir definieren ihn wie folgt.

Sei (p_i,l_i)_{i=1,2,3}\in\mathcal{F}^3_+ ein Tripel von Fahnen. Ein solches ist äquivalent zu einem Paar von ineinander verschachtelten Dreiecken \Delta=(p_1, p_2, p_3) und \Delta'=(q_1, q_2, q_3). Dies kann man gut in der folgenden Abbildung erkennen. Diese Aufteilung induziert drei Vierecke Q_1, Q_2 und Q_3.

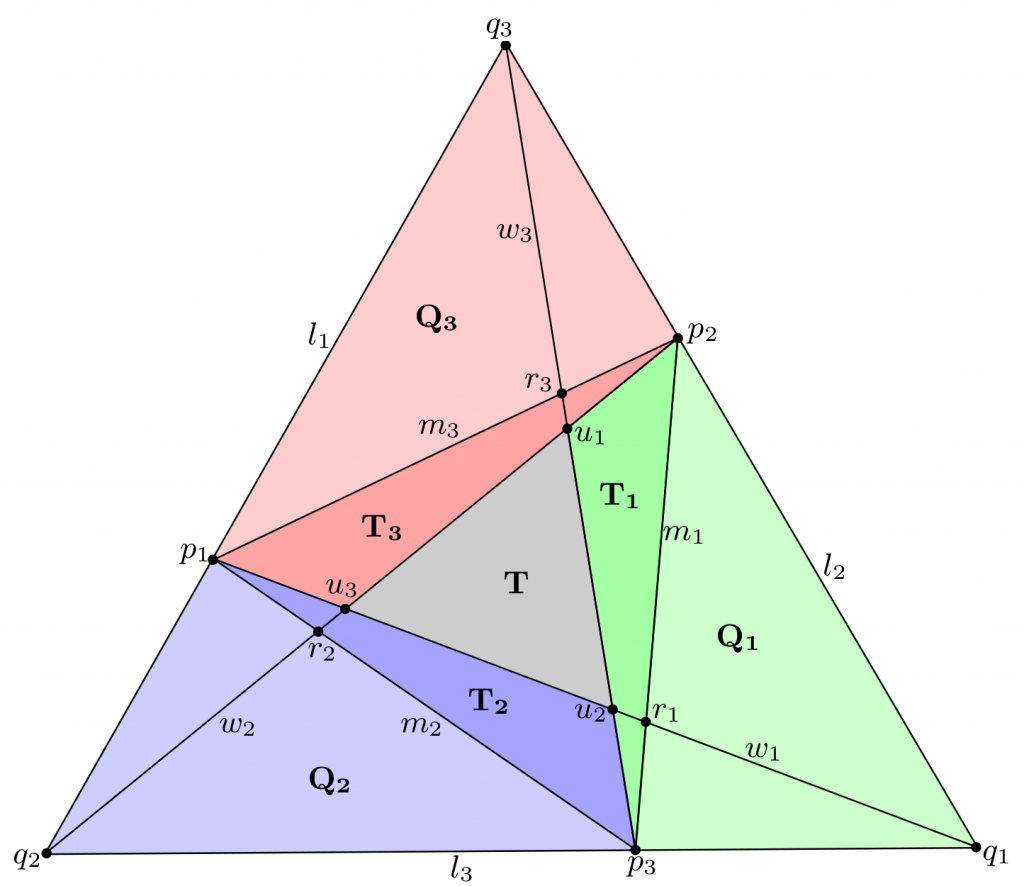
Der Fluss wird nun definiert, indem wir jedes Viereck Q_i mit einem anderen Element von \mathbf{PGL}(3,\mathbb{R}) verformen, nämlich mit

g_1(t) =\begin{pmatrix}1 & 0 & 0\\0 & e^{\tfrac{t}{3}} & 0\\0 & 0 & e^{-\tfrac{t}{3}} \\ \end{pmatrix}, \quad g_2(t) = \begin{pmatrix} e^{-\tfrac{t}{3}} & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & e^{\tfrac{t}{3}}\\ \end{pmatrix}, \quad g_3(t) =\begin{pmatrix}e^{\tfrac{t}{3}} & 0 & 0\\ 0 & e^{-\tfrac{t}{3}} & 0\\ 0 & 0 & 1\\ \end{pmatrix}

wobei alle Matrizen in einer Basis geschrieben wird, die von Repräsentanten der q_1, q_2 und q_3 definiert wird. In der Tat lässt diese Transformation die Punkte q_i invariant. Die transformierten Punkte p_i(t) bleiben auf den Linien l_i. Dadurch liefert die Transformation ein paar verschachtelter Dreiecke \Delta(t),\Delta'(t), das gleichbedeutend mit einem Tripel von Fahnen ist, wie man oben sehen kann.

Visualisierungen des Eruptionsflusses

3D-Druck des ausbrechenden Vulkans

In diesem 3D-gedruckten Modell stellt die Modellhöhe das Fortschreiten von t dar, wohingegen jeder horizontaler Querschnitt (in Grün) das transformierte innere Dreieck T(t) der oben sichtbaren Zerlegung darstellt. Das graue Basisdreieck ist schlichtweg \Delta'.

Verschiedene Fixpunkte des Eruptionsflusses

Je nachdem, wie wir die Matrizen g_i(t) anwenden, kann der Eruptionsfluss verschiedene Fixpunkte haben. Wenn wir die Punkte q_i als Basis für die Matrixdarstellung wählen, werden genau diese Punkte unter der Transformation invariant bleiben. Wenn wir jedoch die Punkte p_i wählen, werden diese zu Fixpunkten, und die q_i bewegen sich. Man kann diesen Unterschied in den Filmen sehen. Der Unterschied ist jedoch kein besonders großer, da sich beide Transformation nur durch ein von t abhängiges Element von \mathbf{PGL}(3,\mathbb{R}) unterscheiden.

Das rote Dreieck ist das, das von den u_i aufgespannt wird, das blaue wird von den p_i aufgespannt, und das schwarze von den q_i. Die Zeit repräsentiert den Transformationsparameter t.

Transformation eines Kreises

Wähle eine Projektion der projektiven Ebene, unter der das äußere Dreieck q_i und das mittlere Dreieck p_i beide gleichseitig sind, und jeder Punkt p_i genau in der Mitte der Geraden des äußeren Dreiecks liegt. Dann ist das durch die u_i aufgespannte innere Dreieck lediglich ein Punkt. In der Tat handelt sich um den Mittelpunkt des Dreiecks. Wir können nun den Inkreis betrachten und seine Transformation unter dem Eruptionsfluss beobachten, was einen guten Eindruck des Flusses liefert.

Mehr über Transformationen von Fahnen

Wir können auch mehr Fahnen transformieren, siehe hier für den Eruptionsfluss auf Viertupeln von Fahnen, sowie andere Transformationen, nämlich den Beulfluss und den Scherfluss.

Die mathematischen Informationen auf dieser Seite kommen aus dem Artikel

Wienhard, A. & Zhang, T. (2017). Deforming convex real projective structures. math.GT; arXiV 1702.00580.