Projektive Geometrie: Transformationen von vier Fahnen

Was ist eine Fahne?

Eine Fahne besteht aus einer Geraden und einem Punkt, der auf dieser Geraden liegt. Wir betrachten Fahnen im zweidimensionalen reellen projektiven Raum. Dies ist eine zweidimensionale Ebene, zu der wir aber alle Punkte im Unendlichen „hinzufügen“. Das heißt, dass wir für jede Menge an parallelen Geraden einen Punkt im Unendlichen hinzufügen, an dem sich die Parallelen schneiden. Wenn wir nun einen bestimmten Teil dieses Raums auswählen, können wir diesen visualisieren, für Details siehe hier. Wir werden verschiedene Transformationen von vier Fahnen betrachten, nämlich den Beulfluss, den Scherfluss und den Eruptionsfluss.

Transformationen von vier Fahnen

Der Beulfluss (engl. bulge flow) und der Scherfluss (engl. shear flow) sind Flüsse auf Tupeln von vier Fahnen.

Betrachte also ein positives Tupel (p_i,l_i)_{i=1,\ldots, 4}\in\mathcal{F}^4_+ von vier Fahnen. Deren Schnittpunkte spannen ein Viereck auf. Ähnlich wie beim Eruptionsfluss auf drei Fahnen wird dieses Viereck in verschiedene Bereiche aufgeteilt, auf die wir jeweils eine Matrix anwenden.

Konvexe Mengen

Tatsächlich definiert ein Tupel aus vier Fahnen zwei ineinander verschachtelte Vierecke: Das äußere Viereck wird von den Schnittpunkten q_i der Geraden aufgespannt, das innere Viereck wird von den p_i aufgespannt. Wir können aus dem inneren Viereck eine konvexe Menge konstruieren, indem wir es entlang seiner Seiten reflektieren. Dieses Verfahren wird unendlich oft wiederholt. Die Reflexion, die gemeint ist, ist eine besondere projektive Reflexion: Stellen Sie sich vor, Sie stünden auf Eisenbahngleisen und sähen einen Punkt v am Horizont, an dem sich die parallelen Gleise treffen. Wenn Sie nun ein auf dem Boden liegendes Viereck entlang einer seiner Seiten l reflektieren, sieht es anders aus als sein bloßes Spiegelbild. Dies liegt an der Perspektive. Als mathematische Formel schreiben wir diese projektive Reflexion als

R(x) = x - l(x)v,

wobei l(\cdot) die Linearform ist, die die projektive Gerade l definiert.

Siehe weiter unten für ein Bild dieser konvexen Menge.

Visualisierungen der verschiedenen Flüsse

Der Beulfluss

In diesem Film sehen wir, woher der Name Beulfluss kommt. Je nach Wahl des Parameters beult sich das ursprüngliche Viereck immer weiter nach links oder rechts aus.

Der Scherfluss

In diesem Film sehen wir, wieso der Scherfluss so heißt. Der linke und rechte Punkt werden verdreht, als ob sie eine Scherkraft erfahren würden. Beachten Sie auch eine weitere interessante Eigenschaft des Scherflusses. Während die zwei mittleren Punkte fest bleiben, bewegen sich der linke und der rechte Punkt zu jeder Zeit auf Ellipsensegmenten.

Die konvexe Menge unter Einfluss des Eruptionsflusses

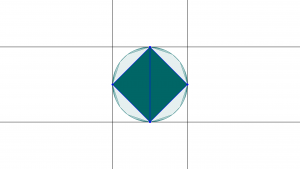
Wir zuvor erklärt, können wir eine konvexe Menge aus einem positiven Tupel von Fahnen konstruieren, indem wir das Polygon entlang seiner Seiten reflektieren. Wenn wir das Polygon nun in mehrere Dreiecke unterteilen, können wir jedes Dreieck mit dem Eruptionsfluss transformieren, und beobachten, was dabei mit der konvexen Menge passiert. Diese Unterteilung in Dreiecke wird im Bild durch blaue Linien dargestellt.

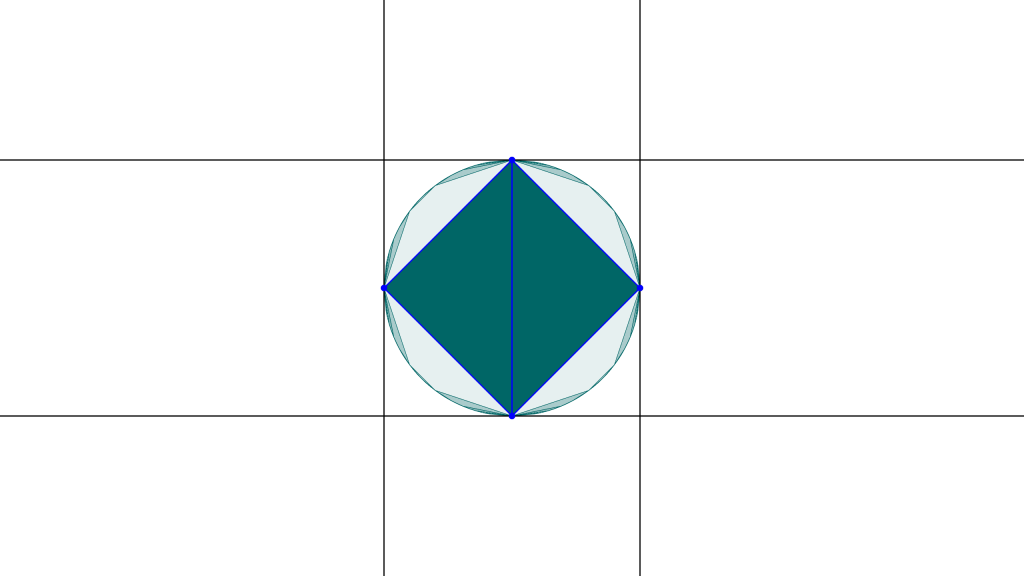
Wir haben nun verschiedene Möglichkeiten, den Eruptionsfluss anzuwenden. Wir könnten ein Dreieck mit einem positiven Parameter t transformieren, und das andere mit einem negativen Parameter {-t}. Stattdessen könnten wir aber auch beide mit einem positiven Parameter t und abermals t transformieren.

Das Ergebnis sieht recht unterschiedlich aus, betrachte

im Vergleich zum folgenden Video.

Beachten Sie, dass wir das Bild üblicherweise mit einer projektiven Transformation, d.h. einem Element von \mathbf{PGL}(3,\mathbb{R}) retransformieren, um die schwarzen Linien fest zu lassen. Wenn wir das nicht tun, „explodiert“ das Bild sehr rasch, wie man unten sehen kann.

Mehr über Transformationen von Fahnen

Die mathematischen Informationen auf diese Seite stammen aus

Wienhard, A. & Zhang, T. (2017). Deforming convex real projective structures. math.GT; arXiV 1702.00580.