Prognosen auf dem Prüfstand

Statistiker aus dem HITS, dem KIT und der Universität Heidelberg haben ein neues Verfahren („CORP“) ​entwickelt, mit dem die Zuverlässigkeit von Prognosemethoden besser diagnostiziert werden kann. Dieser Ansatz ist auch bei der Methodenentwicklung im maschinellen Lernen relevant. Die Studie ist jetzt in den „Proceedings der National Academy of Sciences“ (PNAS) erschienen.

Wenn wir heutzutage das Haus verlassen, werfen wir zuvor noch einen Blick auf das Smartphone. Wenn die Wetter-App meldet: „Mit 60%-iger Wahrscheinlichkeit wird es regnen“, nehmen wir den Schirm mit. Aber wie zuverlässig sind diese Prognosen? Und können wir probabilistische Methoden auch auf anderen Gebieten anwenden, etwa für die wirtschaftliche Entwicklung? So sind zum Beispiel Niederschlagsvorhersagen im tropischen Afrika häufig unzuverlässig – ein wichtiges Thema für Landwirte, die um ihre Ernte bangen. Eine Verbesserung der Prognosemethoden setzt stabile und vertrauenswürdige diagnostische Verfahren voraus, mit denen etwaige Schwachstellen erkannt werden können.

Stabiler und effizienter: Das CORP-Verfahren

Mit diesen Fragen im Hinterkopf und motiviert durch eine kürzlich veröffentlichte Studie zur Niederschlagsvorhersage für das nördliche tropische Afrika entwickelte die Gruppe Computational Statistics am Heidelberger Institut für Theoretische Studien (HITS) unter der Leitung von Tilmann Gneiting einen neuen Ansatz für die Prognosebewertung. In einem jetzt veröffentlichten Artikel in den „Proceedings der National Academy of Sciences“ (PNAS) stellen die Autoren „CORP“ vor (a Consistent, Optimally binned, and Reproducible reliability diagram that uses the Pool-adjacent-violators (PAV) algorithm). Das Ergebnis dieses Verfahrens ist ein grafisches Hilfsmittel, das „CORP-Zuverlässigkeitsdiagramm“, welches stabiler und effizienter ist als die seit Jahrzehnten verwendete klassische Variante.

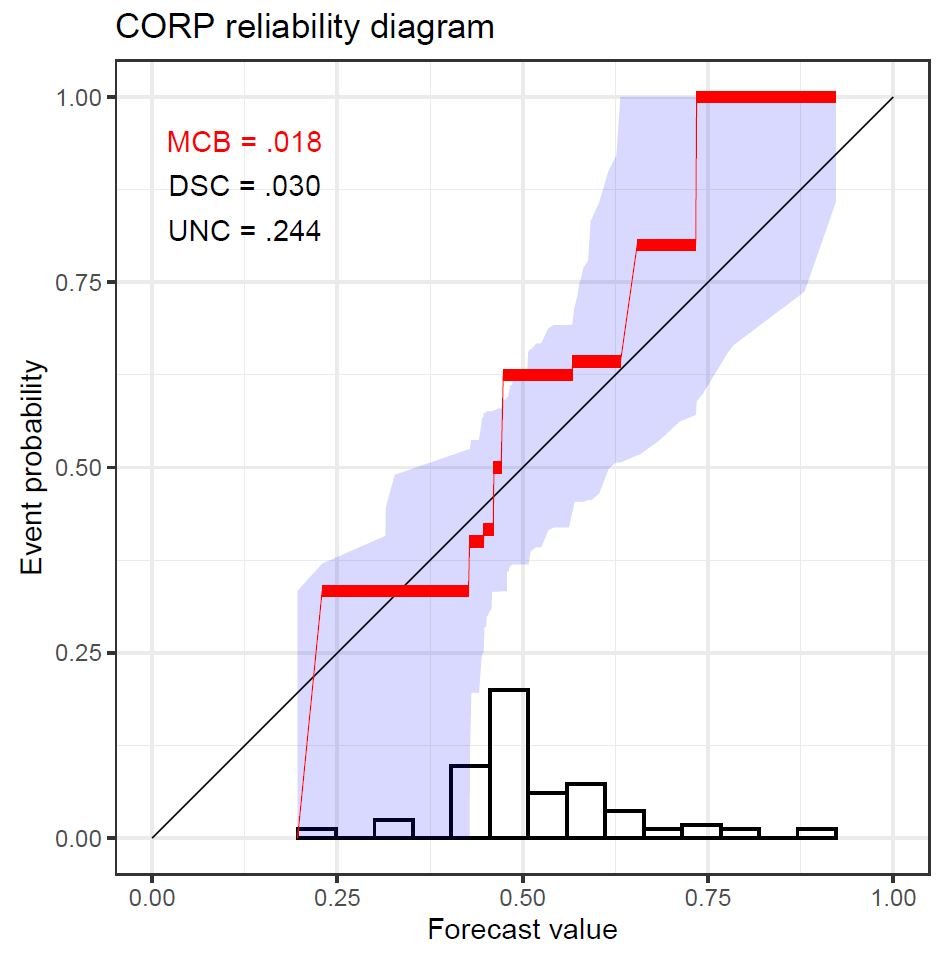
Die Kalibrierung oder Zuverlässigkeit ist von wesentlicher Bedeutung für Wahrscheinlichkeitsprognosen und Wahrscheinlichkeitsklassifikatoren. Ein Klassifikator ist kalibriert oder zuverlässig, wenn die Beobachtungen statistisch mit den Vorhersagen vereinbar sind. Beispielsweise sollte die beobachtete relative Ereignishäufigkeit für Fälle mit einer Vorhersagewahrscheinlichkeit von etwa 80% ebenfalls etwa 80% betragen. „In der Praxis wird Kalibrierung in Zuverlässigkeitsdiagrammen grafisch geprüft und über eine numerische Kennzahl quantifiziert“, sagt Co-Autor Alexander Jordan (HITS).

Seit vielen Jahrzehnten prüfen Wissenschaftler/-innen und Anwender/-innen aus unterschiedlichsten Gebieten die Kalibrierung von Prognosemethoden, wobei das Interesse angesichts der grundlegenden Rolle von Klassifikationsproblemen in künstlicher Intelligenz und maschinellem Lernen in jüngster Zeit stark zugenommen hat. Bisherige Ansätze zum Erzeugen von Zuverlässigkeitsdiagrammen beruhen auf Diskretisierung („binning“) und Zählen („counting“), leiden jedoch unter Ad-hoc-Implementierungsentscheidungen, mangelnder Reproduzierbarkeit und Ineffizienz.

Probleme der „realen Welt“ und mathematische Methoden: Ein fruchtbares interdisziplinäres Zusammenspiel

Der neue CORP-Ansatz basiert auf dem klassischen PAV-Algorithmus, der vor fast 70 Jahren erstmals vorgeschlagen wurde. CORP erlaubt die grafische Überprüfung der Zuverlässigkeit von Wahrscheinlichkeitsprognosen, Das Verfahren ermöglicht „uncertainty quantification“, also die Berechnung von Unsicherheiten im Bewertungsverfahren, und liefert ein neues numerisches Maß für Fehlkalibrierung. Zur Veranschaulichung der neuen Hilfsmittel verwendet die Studie experimentelle Datensätze nicht nur aus der Meteorologie, sondern auch aus der Astrophysik, den Sozialwissenschaften und den Wirtschaftswissenschaften.

Zum Beispiel bewerten die Autoren Wahrscheinlichkeitsprognosen für Rezessionen im US-Bruttoinlandsprodukt (BIP). „Im Gegensatz zum Binning- und Counting-Ansatz erweist sich das CORP-Zuverlässigkeitsdiagramm als stabil, selbst bei schwierigen Prognoseproblemen mit hoher Schätzunsicherheit“, fasst der Erstautor Timo Dimitriadis (jetzt Juniorprofessor für Angewandte Ökonometrie an der Universität Heidelberg) zusammen. Tilmann Gneiting, der auch Professor für Computational Statistics am Karlsruher Institut für Technologie (KIT) ist und dort im Lenkungsausschuss des Zentrums für Mathematik in Naturwissenschaften, Ingenieurwissenschaften und Wirtschaftswissenschaften (MathSEE) sitzt, betont die gegenseitigen Vorteile interdisziplinärer Forschung am Beispiel dieser Studie: „Mathematische und statistische Methoden dienen als Werkzeuge zur Lösung wichtiger Probleme der realen Welt, während wichtige Probleme der realen Welt neue methodische Entwicklungen in Mathematik und Statistik hervorbringen.“

Die Autoren rechnen damit, dass ähnlich gelagerte Anwendungen des PAV-Algorithmus zu verbesserter Diagnostik und Inferenz bei einer Vielzahl von Methoden der Statistik und des maschinellen Lernens führen. Der Artikel wurde am 23. Februar 2021 in den “Proceedings of the National Academy of Sciences of the United States of America” (PNAS) veröffentlicht.

Timo Dimitriadis, Tilmann Gneiting, and Alexander I. Jordan: Stable reliability diagrams for probabilistic classifiers​, PNAS, February 23, 2021 118 (8) https://doi.org/10.1073/pnas.2016191118