Hyperbolische und euklidische Geometrie vergleichen
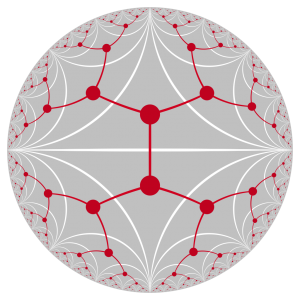
Parkettierungen der hyperbolischen und der euklidischen Ebene
Hyperbolische und euklidische Geometrie haben einen recht individuellen Geschmack. Sie unterscheiden sich deutlich voneinander. Man kann das gut erkennen, indem man Parkettierungen, oder Kachelungen, dieser beiden Geometrien vergleicht. Betrachte also eine Parkettierung der euklidischen Ebene mit Quadraten, und eine Parkettierung der hyperbolischen Ebene mit idealen Dreiecken. Wir zeichnen dann einen Graphen, der bildhaft macht, welche Kacheln aneinander grenzen. Im Falle der euklidischen Geometrie handelt es sich um ein schlichtes Gitter. Im Falle der hyperbolischen Geometrie wird es jedoch ein Baum, der sich in jeder Richtung unendlich fein verästelt.
Wir haben das Poincarésche Scheibenmodell verwendet, um die hyperbolische Ebene zu visualisieren.

Kachelung der euklidischen Ebene mit Quadraten. 
Graph (in Rot), der die aneinander grenzenden Kacheln visualisiert.

Kachelung der hyperbolischen Ebene mit idealen Dreiecken. 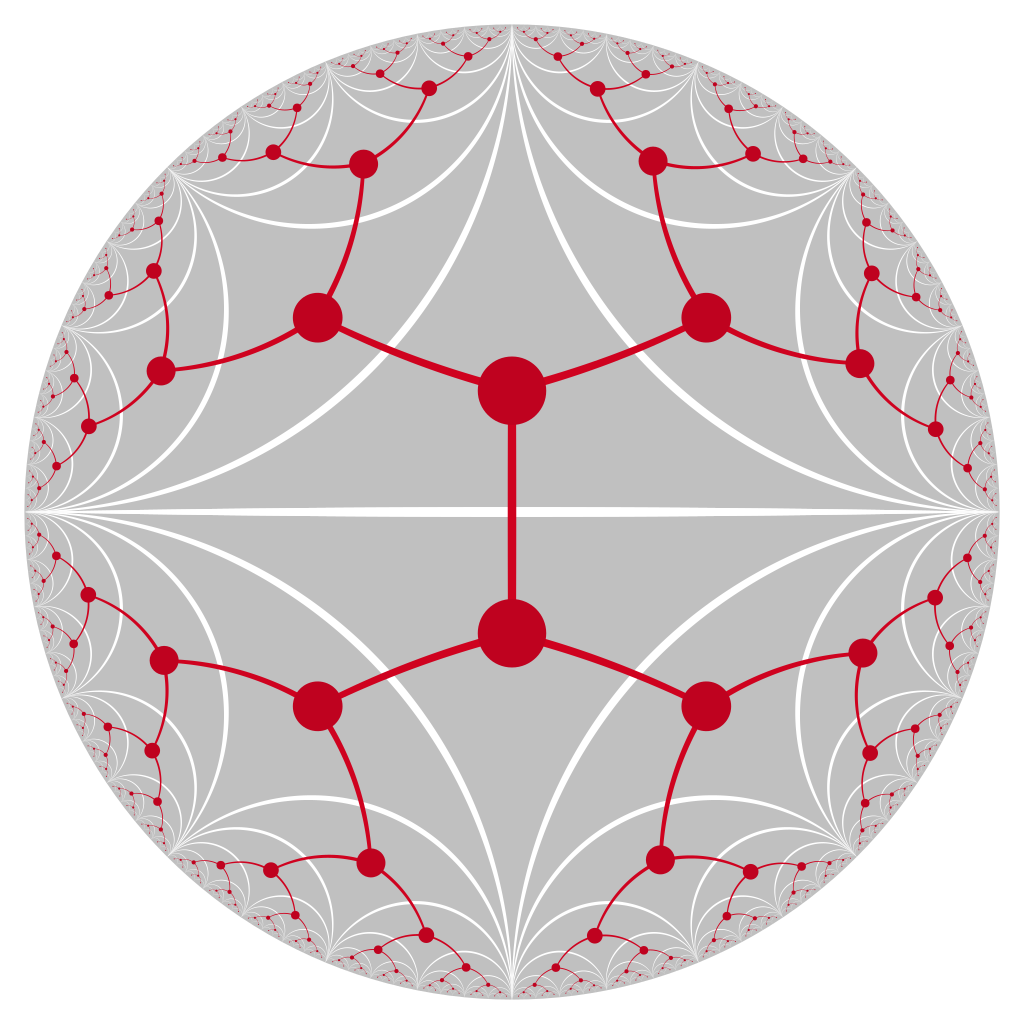
Graph (in Rot), der die aneinander grenzenden Kacheln visualisiert.
Der approximierende Graph in der hyperbolischen Ebene
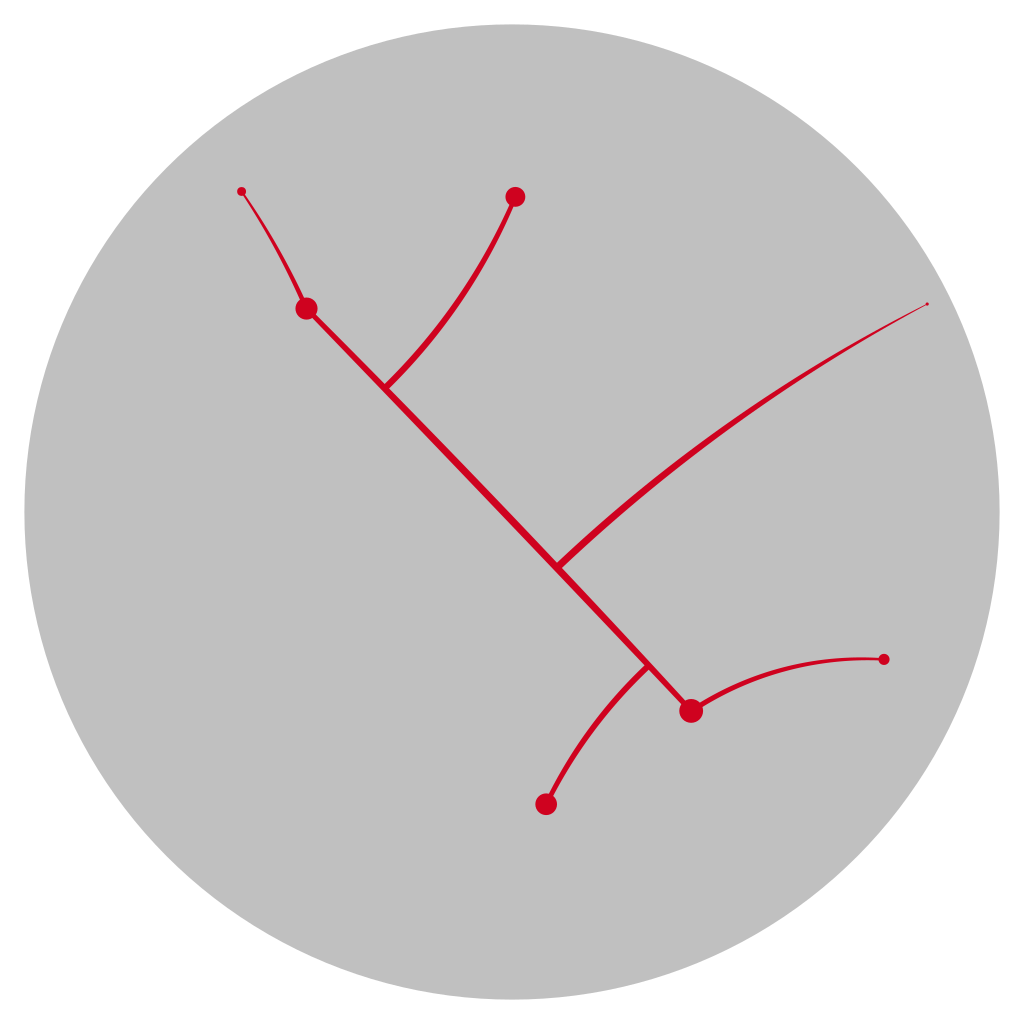
Wählen Sie eine endliche Menge von Punkten in der hyperbolischen Ebene, quasi eine „Punktewolke“. Der „kürzeste Weg“, oder korrekter eine Geodäte zwischen zwei dieser Punkte ist im Poincaréschen Scheibenmodell ein Kreissegment. Wenn wir jedes beliebige Paar von Punkten mit der jeweiligen Geodäte verbinden, erhalten wir ein ziemliches Netz aus Linien. Erfreulicherweise können wir dieses Netz durch einen approximierenden Graphen vereinfachen: Es gibt einen Graphen, dessen Kanten Geodäten sind, und dessen Knoten alle Punkte unserer Punktewolke enthalten. Das besondere ist, dass es nicht „wesentlich länger“ ist, entlang der Kanten des Graphen von einem Punkt zum anderen zu gehen als auf dem direkten Weg. Die Distanz unterscheidet sich um einen Fehler, der nur von der Anzahl der Punkte n abhängt:
d_\mathrm{tree}(x, y) \leq d(x,y) + f(n).Für die Konstruktion des Graphen haben wir einen sehr einfachen Algorithmus verwendet: Die erste Kante ist einfach die Geodäte, die die ersten beiden Punkte verbindet. Danach wählen wir immer einen Punkt in der Wolke, der noch nicht mit dem Graphen verbunden ist. Wir suchen den Punkt auf dem Graphen, der dem gewählten Punkt am nächsten ist. Dann fügen wir die Kante zwischen den beiden Punkten hinzu. Das Ergebnis kann man unten sehen.
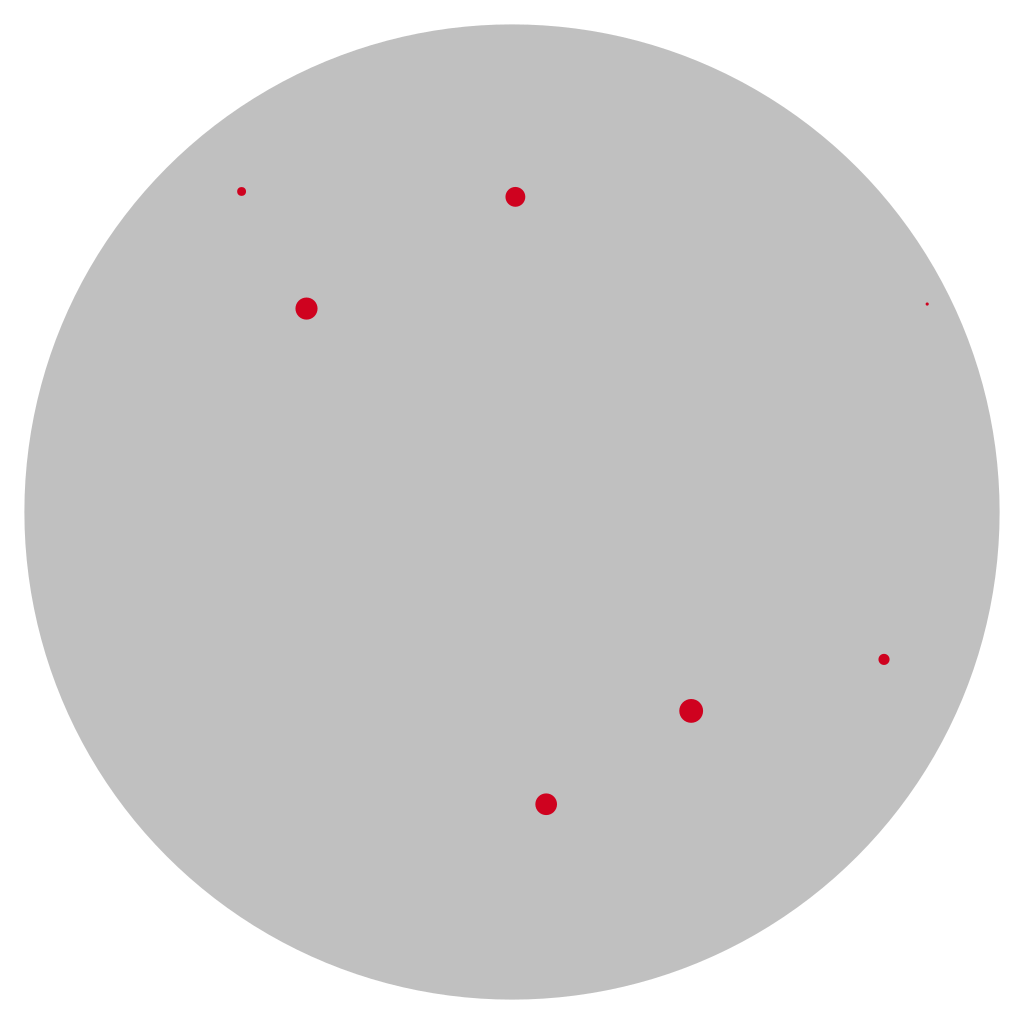
Eine Punktewolke in der hyperbolischen Ebene. 
Alle Geodäten, die Paare von Punkten verbinden, und der approximieren Graph zum Vergleich.